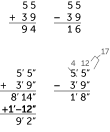
If you ask people on the street, “how much is 5 feet 5 inches and 3 feet 9 inches,” most would get it wrong. Here’s why.
When you add “decimally,” like dollars and cents, “carry the one” means converting ten in the ones column to one in the tens column. But that’s not how feet and inches works. You don’t carry a decimal’s worth of ones with feet and inches, you carry a dozen. Roman v. Celtic.
The prime or double prime characters illustrate this point. In the trades, a prime character means feet, a double prime character means inches. So the difference between the top problems and the bottom two, is that the top numbers are “decimal,” and the bottom two are feet & inches. The bottom two read, “five feet, five inches” and “three feet, nine inches.” These are not decimal numbers, and should never be read as “five point five,” or “three point nine.”
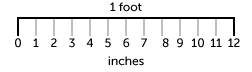
Once again, 12 inches, not 10, equals a foot.
Let’s look more closely at how borrow/carrying works with feet and inches.
Adding
The left problem reads, “five feet, five inches, plus, three feet, nine inches.” First, add the feet together, add the inches together. Eight feet, fourteen inches. Since we now have 12 or more inches, we can convert a bundle of twelve inches into a foot. That’s what the +1′ –12″ line of the problem means — carry twelve inches away from the 14 inches, and make it a foot. Add the 12 inch bundle to the feet, converting 8′ 14″ into 9′ 2″, final answer.
Subtracting
Breaking a foot into a bundle of a dozen inches when subtracting requires moving the 12 inch bundle before doing the subtracting — you can’t take away 9 inches from 5 inches, so borrow a foot, a dozen inches, and add it to the 5 inches you already have. Adding a foot (12 inches) to the 5 inches we already have gives us 17 inches. So 5′ 5″ converts to 4′ 17″. Now take away the 3′ 9″, and you get 1′ 8″, final answer.
What if you add up to less than 12 inches, or your top inch number is greater than your bottom inch number when subtracting? Then you don’t need to borrow or carry, just do the calculation and you’re done!
The Funnel Technique
Drawing with a carpenter’s pencil, on a stud or dry wall, is a quick and dirty way to figure out a trades math problem, like the perimeter of a room. But an “are you Smarter than a Fifth Grader” question is either right or wrong. You add up the sides wrong, and you’ll have the wrong amount of material to get the job done, and, more importantly, you’re wasting time. There is a technique to adding up multiple sides to help make sure your answer is error free. It’s called the “funnel technique.” Consider how to figure out the perimeter of the shape below.

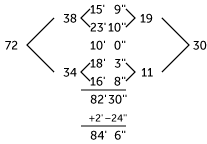
The best way to add up a bunch of feet and inches is to stack them up, and, as illustrated to the right, add a pair of numbers, and then another, until all of the inches, and all of the feet, have been added up to one total number. Then, apply the “carry” rule we learned in the last lesson to simplify the final answer. In this problem, 24 inches, or 2 feet, can be carried from the inches column into the feet column.



